Чим займаються теоретики - розширення теорії

Падіння тіла із початковою швидкістю -- розраховуємо більш складну систему

Спробуємо розширити застосування нашої теорії на випадок, коли початкова швидкість не дорівнює нулю:\[v_0\neq0.\] Повторимо міркування з попередньої статті:

t	v	l
0	\( v_0 \)	0
\(\Delta t\)	\(v_0 + g \Delta t\)	\(v_0 \Delta t\)
\(2\Delta t\)	\(v_0 + 2 g \Delta t\)	\(v_0 \Delta t + g \Delta t^2 \)
\(3\Delta t\)	\(v_0 + 3 g \Delta t\)	\(v_0 \Delta t + 2 g \Delta t^2 \)
\(4\Delta t\)	\(v_0 + 4 g \Delta t\)	\(v_0 \Delta t + 3 g \Delta t^2 \)
\(5\Delta t\)	\(v_0 + 5 g \Delta t\)	\(v_0 \Delta t + 4 g \Delta t^2 \)
і т.д.

Розраховуємо повне переміщення, майже так само, як раніше: \[L=v_0 \Delta t + v_0 \Delta t + g \Delta t^2 + v_0 \Delta t + 2 g \Delta t^2 + \\ + v_0 \Delta t + 3 g \Delta t^2 + \ldots + v_0 \Delta t  + (N-1) g \Delta t^2,\] де \(N = \frac{t}{\Delta t}\) -- кількість проміжків \(\Delta t\), які складають наш час t. Доданки із g не змінилися, тому, після підсумовування, дадуть все те ж: \( g \frac{t^2}{2} - g  \frac{t \Delta t  }{2}\). Крім них залишилося N доданків: \[v_0 \Delta t + v_0 \Delta t + v_0 \Delta t  + \ldots + v_0 \Delta t = v_0 N\Delta t = v_0 t.\] Отже: \[L=v_0 t + g \frac{t^2}{2} - g  \frac{t \Delta t  }{2}, \] і в границі як завгодно малого \( \Delta t\):\[L=v_0 t + g \frac{t^2}{2}.\]

Тепер ми можемо розв'язувати новий клас задач, які безпосередньо стосуються реальності, наприклад, дослідження польоту тіл, підкинутих вверх. Детально їх тут не розглядатимемо, хоча в процесі такого розгляду можна зустріти декілька цікавих нюансів. :-)

Переходимо у два виміри -- узагальнення нашої теорії

 

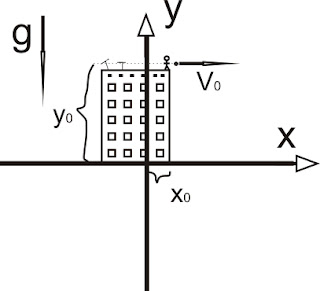
Наша теорія падіння тіл все ж доволі вузька. Вона описує лише рух тіл вздовж лінії, що з'єднує тіло з центром планети -- вертикальне падіння. А якщо розглянути, наприклад, тіло, викинуте з відмінної від нуля горизонтальною швидкістю? Щоб справитися з цією задачею, доведеться знову залучити загальну теорію. Як відомо: \[\vec{F}=m\vec{a}.\] В цьому місці, нарешті, дуже варто ввести систему координат. Фактично, ми неявно користувалися нею і раніше, але тепер такої неявної присутності недостатньо(*). Розташуємо осі так, як на рисунку(**). Тоді, завдяки векторній природі рівняння вище (див. також першу нотатку циклу), можна його записати як два незалежних рівняння вздовж кожної із осей: \[F_x=0, \\ F_y =m g,\] де m -- як і раніше, маса нашого тіла. Друге рівняння відповідає якраз тій задачі, що ми вирішили минулого разу -- падінню під дією сили тяжіння, перше -- вільному руху тіла по горизонталі. Як бачимо, наша задача розпалася на дві незалежних -- вже досліджене падіння, та рух тіла без прискорення. Тобто, вздовж осі y рух описується отриманим раніше співвідношенням, а вздовж x -- ним же, але з нульовим прискоренням. (Звичайно, можна вивести ще раз, але лінь. :) Нехай в початковий момент тіло матиме координати, як на рисунку: \((x_0,y_0)\), та швидкість \(v_{x,0}, v_{y,0}\), тоді його рух описують наступні співвідношення:\[x=x_0+v_{x,0} t, \\ y=y_0 + v_{y,0}t - \frac{g t^2}{2},\] де прискорення від'ємне, так як направлене у протилежному напрямку до вибраного напрямку осі y.

Отримана розширена теорія може описувати значно більше коло задач, ніж попередня. Правда, всі обмеження попередньої теорії щодо області застосування -- нехтування опором повітря і т. д., залишаються. 

Розглянемо, як вона може застосовуватися на цілком реальній задачі (випадок на будівництві у Жидачеві, десь в 80-х роках): людина йде по периметру щойно побудованого четвертого поверху (висотою, скажімо, 3*4=12 метрів), стіна повертає, людина (по п'яні) продовжує йти прямо. Питання, наскільки далеко від будинку вона впаде? (Що цікаво, дядько відбувся переломом ключиці, після інциденту швидко-швидко втік з лікарні). Нехай її швидкість -- \(v_{x,0}=5 км/год \approx 1.4 м/с \).

Визначимо час польоту. Вираз для нього вже отримано раніше:\[t=\sqrt{\frac{2h}{g}}.\] Віддаль, яку пролетить людина за цей час:\[L=v_{x,0}*t = v_{x,0} \sqrt{\frac{2h}{g}} = 1.4 *  \sqrt{\frac{24}{9.8}}\approx1.4*1.56=2.19 м.\] Як бачимо, ні віддаль (трішки більше двох метрів, ні час падіння - півтори секунди) не вражають. :-)

Врахування опору повітря -- емпіричне розширення теорії(***)

Для багатьох задач нехтувати опором повітря не можна. Навіть автомобілі відчувають його доволі помітно. На жаль, загальна теорія руху тіл в повітрі (і загальніше -- в середовищах) -- надзвичайно складна, конкретних аналітично розв'язаних задач небагато, а чисельні дослідження вимагають великих зусиль. Однак, експериментально показано (****), що сила опору повітря, для даного тіла, при відносно невеликих швидкостях, пропорційна квадрату його швидкості:\[F_s=C v^2,\] де C -- коефіцієнт, який залежить від площі перерізу тіла, густини середовища і т. д.

Ввівши таке емпіричне розширення, можна з високою точністю розраховувати падіння тіл, для яких нехтувати опором повітря неприпустимо. Однак, слід відрізняти такі напів-емпіричні теорії, від строго виведених в рамках якоїсь загальнішої теорії, хай і з застосуванням наближень. 

Розглядатимемо, для простоти, лише одномірну задачу. Додаткова складність тут така, що в залежності від напрямку руху, сила тертя може бути направлена і вверх і вниз. Для ясності, розглянемо падіння -- напрямки сили тяжіння і сили опору повітря протилежні. Повна сила, що діє на тіло: \[F=mg-C v^2, \] згідно другого закону Ньютона: \[m a = m g - C v^2, \] \[a = g - C \frac{v^2}{m},\] тобто тепер прискорення залежить від маси. 

Розв'язати це рівняння аналітично можна, але це буде багато складніше, ніж раніше. Однак, цікаві висновки про рух тіл в повітрі, можна зробити навіть не маючи кінцевого виразу. Спробуємо спочатку розв'язати чисельно, за допомогою невеликої модифікації використаної раніше програми:

t_end=5; -- Момент закінчення
g=9.8; -- Прискорення вільного падіння

x=0; -- Початкове положення
t=0; -- Початок відліку часу
v=0; -- Початкова швидкість
delta_t=0.01; -- Крок по часу

C=0.1 -- Коефіцієнт опору повітря
m=1 -- Маса

print(string.format( "t\tx\tv", t, x, v) );
while t<=t_end-0.00000000001 do -- щоб зупинитися рівно у 5 секунд
-- На жаль, через похибку заокруглення просто t<=t_end не працює
-- зупиняючись на t=5.05
   v = v+(g - C*v^2/m)*delta_t; -- Зміна швидкості за час delta_t
   x = x+v*delta_t; -- Зміна положення за цей же час

   t = t+ delta_t; -- Переходимо до наступного моменту

    print(string.format( "%.4f\t%.4f\t%.4f", t, x, v) );
end

Коефіцієнт C вибрано менш-більш довільно -- розрахунки служать виключно для ілюстрації. Побудуємо графік швидкості в залежності від часу польоту:

Чисельний аналіз показує цікаву закономірність -- спочатку швидкість зростає майже лінійно, як і без опору повітря, (тому до певних швидкостей опором повітря можна нехтувати, як ми й робили), однак потім зростання швидкості зупиняється та вона залишається фактично постійною. Тобто, тіло починає рухатися рівномірно, а значить сумарна сила, що діє на нього, (доволі швидко), стає рівною нулю. Справді -- росте швидкість, з її зростанням збільшується опір повітря, поки не зрівноважує силу тяжіння. При цьому наше рівняння набуває такого вигляду: \[0 = g - C \frac{v^2}{m},\]з якого можна знайти швидкість падіння, що встановиться: \[v=\sqrt{\frac{m g}{C}}.\]

Наприклад, швидкість парашутиста зростатиме лише невеликий проміжок часу, а потім він рухатиметься із постійною швидкістю, яку можна вирахувати, знаючи коефіцієнт C для парашута.

Тобто, наша теорія дає цілком конкретні передбачення, хоча й рівняння руху -- залежність положення від часу, ми поки не знайшли.

Ось приблизно так робота фізика-теоретика і виглядає, але на багато складніших системах. В цій серії нотаток використав таку, тривіальну і загальновідому, систему, щоб технічні труднощі сприйняття не відволікали від структури роботи. Можливо, колись розглянемо й більш реалістичні приклади.

---

Виноски

(*) Поняття системи координат вже не розжовуватиму -- лінь, будемо вважати, всі з ним знайомі, в достатній для практичного використання мірі.

(**) Звичайно, простір трьохмірний, і нам знадобилася б ще й вісь z, однак у нашому випадку ніяких сил, перпендикулярних до осі y немає, значить проекція руху тіла на площину, перпендикулярну до z буде пряма -- ніщо не повертатиме його. Тому зручно вісь x вибрати вздовж цієї прямої і обмежитися двомірною системою координат.

(***) Ще одне можливе розширення: використавши емпіричний закон для сили тертя ковзання, можна описати, наприклад, рух тіл по похилих площинах. Залишимо його на домашнє завдання читачам. :-)

(****) Якщо строго, то походження тієї закономірності не таке просте, зокрема згадується закон Стокса. Очевидно, що її можна отримати і аналітично, акуратно застосовуючи відповідні наближення до загальної теорії.